이번 포스팅에서는 Union Find에 대해서 알아보려고 합니다.
Union Find란?
Union Find란 상호 배타적 집합을 표현하기 위해 사용되는 자료구조 입니다.
상호 배타적 집합이라는 표현에 대해서 조금 더 자세하게 설명해보겠습니다.
상호 배타라는 단어는 "서로 겹치지 않는다" 라는 의미이고, 집합은 구별되는 요소들의 모임입니다.
즉 부분집합들이 공통 요소를 가지지 않음을 표현하는 단어가 상호 배타적 집합입니다.
머릿속으로 위 문장을 그려보시면 아래와 같은 그림을 그리실 수 있습니다.

각각의 요소들은 서로 다른 집합에 포함되어 있고, 각 집합들은 교집합을 가지지 않습니다.
Union Find에서는 각 요소들을 0 ~ n-1로 표현합니다.
Union Find의 3가지 연산은 다음과 같습니다.
- 초기화 : n개의 원소들이 각각의 집합에 포함되어 있도록 초기화
- union : 두 원소 a,b가 주어질 때 이들이 속합 집합을 하나로 합침
- find : 원소가 속한 집합을 반
표현방법
표현 방법은 2가지 존재합니다. 배열 과 트리인데 저는 트리로 구현하려고 합니다.
배열로 작성하는 방법의 문제점 때문인데요. 일단 배열로 작성한다고 가정해보겠습니다.
belongsTo[i] = i번 원소가 속하는 집합의 번호
배열의 경우 find는 시간복잡도를 항상 O(1)로 유지할 수 있습니다.
하지만 배열로 작성하게 되는 문제점은 union에서 드러납니다.
모든 union을 하려면 한쪽 집합에 있는 모든 요소들을 다른 쪽 집합들로 옮겨주어야 하는데 이 과정을 코드로 표현하면 시간복잡도가 O(n)이 됩니다.
배열을 이용하면 find는 빠르지만 union은 배열의 특성상 O(n)이라는 시간복잡도를 가지게 됩니다.
그래서 조금 더 어렵지만 성능이 좋은 트리 방식을 통해 상호 배타적 집합을 표현하려고 합니다.
트리로 표현된 상호 배타적 집합
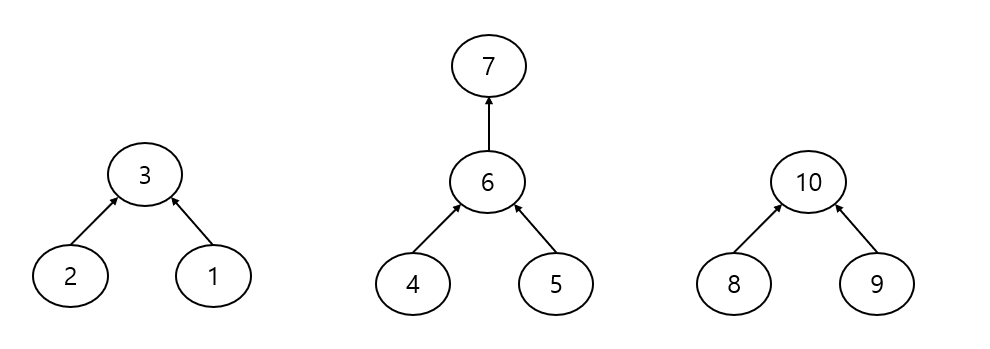
각 원소들을 트리로 묶어주는 방식으로 상호 배타적 집합을 표현합니다.
트리는 부모와 자식은 반드시 1대1로 관계하기 때문에 루트 노드와 그 자식들은 무조건 1대1 대응됩니다.
이 특성을 이용해서 해당 원소가 어느 트리에 속해있는가를 찾아낼 수 있습니다.
코드를 작성해보면 다음과 같습니다.
public class UnionFind {
private int[] parent;
public UnionFind(int size) {
parent = new int[size];
for (int i = 0; i < size; i++) {
parent[i] = i;
}
}
//a 가 속한 트리의 루트 노드 반환
public int find(int a) {
if(parent[a] == a) return a;
else return parent[a] = find(parent[a]);
}
//a와 b가 속한 각 두개의 트리를 합침
public void union(int a,int b){
int Fa = find(a);
int Fb = find(b);
if(Fa != Fb) parent[Fb] = Fa;
}
}
문제점
트리의 특징 중 하나는 입력에 따라 트리의 형태가 달라질 수 있다는 것입니다.
모든 입력이 균형 잡힌 트리를 만들어준다면 좋겠지만 그럴 수가 없습니다.
최악의 경우를 생각해보면 0 과 1 을 합치고, 1과 2를 합치고, 2와 3을 합치고 ...
이렇게 n-1 까지 합쳐본다고 생각하면 트리의 높이가 n이 됩니다.
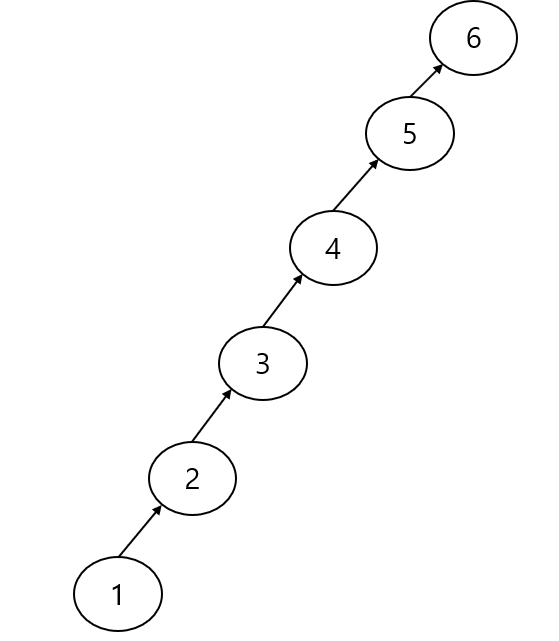
이런 형태의 트리가 만들어진다면 find의 시간복잡도는 O(n) 이 됩니다.
union은 find를 호출하기 때문에 union의 경우도 O(n)이 되어버립니다.
이렇게 되면 배열을 사용할 때보다 더 안 좋은 상황이 됩니다.
최적화
트리가 높아지는 상황을 막을 수 있는 방법 중 가장 쉬운 것은 두 트리를 비교해서 더 낮은 높이를 가진 트리를 높은 트리 밑으로 집어넣는 것입니다.
public class UnionFind {
private int[] parent;
private int[] rank;
// 초기화: 각 원소는 자신을 부모로 가지고, 랭크는 0으로 초기화
// rank는 트리의 높이를 표현
public UnionFind(int size) {
parent = new int[size];
rank = new int[size];
for (int i = 0; i < size; i++) {
parent[i] = i;
rank[i] = 0;
}
}
public int find(int a) {
if(parent[a] == a) return a;
//경로 압축!
//루트를 찾기 위해 방문했던 노드들을 루트에 직접 연결
else return parent[a] = find(parent[a]);
}
public void union(int a, int b) {
int rootA = find(a);
int rootB = find(b);
// 보다 더 높은 높이를 가진 트리 밑으로 낮은 높이의 트리를 넣음
if (rootA != rootB) {
if (rank[rootA] > rank[rootB]) {
parent[rootB] = rootA;
} else if (rank[rootA] < rank[rootB]) {
parent[rootA] = rootB;
} else {
parent[rootB] = rootA;
rank[rootA]++;
}
}
}
}
아래 그림과 같은 형태가 그려집니다.

정리
트리를 이용해 구현한 Union Find 자료구조를 통해 상호 배타적 집합을 표현
부모와 자식은 1대1 대응한다는 트리의 정의를 이용
특정 입력에 의해 트리의 높이가 노드의 수만큼 늘어나는 상태를 방지하기 위해 높이 최적화 기법 사용
